Het belangrijkste nadeel van analoge technieken voor opslag en transport van audio signalen is dat het signaal onderweg van microfoon tot luidspreker bij iedere tussenstap een beetje degradeert. Er komt wat ruis bij en er komt wat vervorming bij. In versterkers en regelapparatuur valt dit allemaal wel mee maar bij het analoog opslaan van de informatie (magneetband, grammofoonplaat) en radio overdracht gaat er  flink  wat verloren.

Digitale technieken hebben dit probleem niet. Het digitale signaal kan zodanig getransporteerd en opgeslagen worden dat er onderweg geen enkele degradatie optreedt, ook niet een heel klein beetje. 

Daarnaast is het in de digitale techniek mogelijk om een klein beetje extra informatie toe te voegen, waardoor aan de reproductie kant eventuele fouten ontdekt en meestal ook perfect gerepareerd kunnen worden. In de analoge wereld kennen we zulke foutcorrectie mechanismes niet.

Omdat analoog veelal met de vinyl-langspeelplaat (LP) geassocieerd wordt en digitaal met de Compact Disk heb ik de eigenschappen van deze systemen even naast elkaar gezet.

Let op: Dit zijn de eigenschappen van deze veelvoorkomende systemen. Niet de eigenschappen van "Analoog" of  "Digitaal" in het algemeen.

De Analoog naar Digitaal omzetting is een twee-stappen proces. Deze stappen zijn van geheel verschillende aard, en er treden dan ook geheel verschillende principiele en praktische fouten op.

De eerste stap is het discretiseren in de tijd. We noemen dit ook wel het sample-proces. De principiele en praktische fouten die hierbij optreden hebben allemaal te maken met het gedrag van de amplitude-frequentie karakteristiek en de tijd responsie. Ook Jitter doet hier z'n invloed gelden.

De tweede stap is het discretiseren in amplitude. Hier hebben we principieel te maken met de kwantiserings-ruis en in de praktijk met enkele niet-lineariteiten.

Het analoge signaal wordt op regelmatige tijdsmomenten gemeten en die waardes worden analoog vastgelegd met een sample-and-hold circuit.

We zien het signaal in fig. 1 als een golfvorm op de horizontale tijd-as. De blauwe lijnen stellen de sample momenten voor en de gearceerde staven geven het signaal op de uitgang van het sample-and-hold circuit weer.

Fig 1.

Op dit punt is het belangrijk om te kijken wat er in het frequentie domein gebeurt.

Fig 2.

Hier zien we op de horizontale as de frequenties staan, de vertikale as geeft de amplitude aan. Het trapezium stelt het gebied voor waarin het audio signaal zich kan bevinden. (In elk stukje muziek is het natuurlijk anders, maar het komt nooit buiten deze grenzen)

Je ziet dat er bij ongeveer 20 Khz geen signaal meer is. (Dat heb ik even aangenomen, we zullen verderop zien waarom)

Na het sampelen met 44 kHz ziet het er zo uit: (n.b: KHz in het plaatje moet  kHz zijn)

Fig 3.

We zien het oorspronkelijke spectrum herhaald terug vanaf elk veelvoud van de sample frequentie, en ook nog eens daaromheen gespiegeld (voorbij de 132 kHz gaat dit patroon gewoon verder, maar zover reikt mijn tekening niet)

Sampelen is nl. een vorm van moduleren. En bij modulatie treden som-en verschilfrequenties op.

Voor degenen die weten wat een Fourier transform en een convolutie is: Het sample proces betekent in het tijdsdomein vermenigvuldigen met een kam-functie met interval t. De Fourier transform van een kam-functie is wederom een kam-functie, nu met de tanden op veelvouden van de sample frequentie (1/t). Vermenigvuldigen in het tijdsdomein betekent convolueren in het frequentie-domein (en v.v.)

Nou, kijk maar eens wat er gebeurt als we in het oorspronkelijke signaal frequenties boven de 20 kHz toelaten (rood):

Fig 4.

Je ziet dat frequenties boven de halve sample frequentie gespiegeld terugkeren in het basisband gebied. Een frequentie van bijv. 30 Khz komt terug als 44 -30 = 14 Khz.

Dit verschijnsel heet "Aliassing" en zo'n teruggevouwen frequentie heet een "Alias". Het is niet mogelijk om achteraf aliassen weg te filteren.

Het is duidelijk dat we dit niet willen. De enige weg is om er voor te zorgen dat er in het te sampelen signaal geen frequenties zitten hoger dan die halve sample frequentie.

Er is dus een analoog laag-doorlaatfilter nodig dat frequenties boven 20 kHz rigoreus onderdrukt, maar frequenties tot 20 Khz ongeschonden doorlaat.

Helaas is zo'n filter erg lastig te maken met analoge middelen (weerstanden, condensatoren, zelfinducties) maar we zullen verderop zien dat er toch een fraaie mogelijkheid is om dit te realiseren.

Dat komt omdat men toen al wist dat er een goede oplossing voor dit probleem is. In de digitale techniek kunnen we nl. veel mooiere filters maken, waarvan de eigenschappen bovendien niet afhankelijk zijn van de toleranties van weerstanden, condensatoren en zelfinducties.

De oplossing is deze: Verhoog de sample frequentie een factor 4 of  8 of noem maar op, flink wat. Het analoge anti-alias filter wordt nu veel eenvoudiger. Maak vervolgens in digitale techniek een mooi alias-filter voor zo'n 21 kHz en voer -wederom digitaal- een hersampling uit op 44.1 kHz

Fig 5

In deze figuur zie je een voorbeeld met 3-voudige oversampling. (Er wordt meestal meer gebruikt, maar dan wordt m'n  tekening zo groot)

In groen staat de benodigde karakteristiek van het analoge alias filter.

In blauw staat die van het digitale filter. Het filtert  het rode signaal weg, in ieder geval voorbij de 22 Khz.

Na hersampling op 44 kHz onstaan uiteraard weer alle zijbanden op veelvouden van 44 kHz, maar die overlappen elkaar niet meer, net zo als in fig 3.

In de praktijk worden sample frequenties tot zeker 256 x 44.1 kHz gebruikt. Een bijkomend voordeel is dat bij deze hoge oversample frequenties de amplitude-discretisering met minder resolutie (aantal bits) kan plaatsvinden. Na de digitale filtering wordt toch de 16-bit resolutie weer gehaald. Ultimo kan een z.g. 1-bit A/D converter gebruikt worden. Hieraan zijn enkele praktische voordelen verbonden. Ik kom daar verderop op terug.

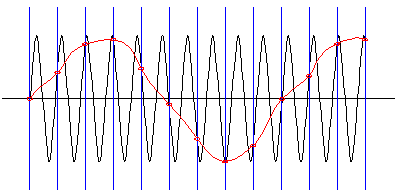
Fig 5a

Je ziet hier in de tijd wat er gebeurt als de signaal frequentie hoger is dan de halve sample frequentie (hier zelfs iets hoger dan de hele samplefrequentie).
Er wordt alleen op de blauwe lijnen gekeken hoe groot het signaal is, en daardoor ontstaat er een volstrekt fout digitaal signaal. 

Kanttekeningen (pdf, 747 kB)  is in 1981 verschenen in het tijdschrift Elektronica,  en het engelstalige artikel Temporal Decay (pdf, 215 kB) is gepubliceerd door de AES.

Er is nu een software programma beschikbaar waarmee je zelf mogelijk wat experimenten kunt doen i.v.m. aliassing en zo.

Om het gesampelde signaal als een reeks getallen te kunnen versturen of opslaan moeten we aan de amplitude van elk sample een getal toekennen. Bij de CD-techniek is gekozen voor 16-bit binaire getallen. Deze hebben een bereik van -32768  tot + 32767. De waarde nul (geen signaal) wordt in het midden gelegd. 

Aangezien het gesampelde signaal nog steeds analoog is kan het elke waarde hebben, ook waardes die tussen de mogelijke getallen in liggen: Als we discrete getallen gaan toekennen zullen er dus afrondingsfouten ontstaan.

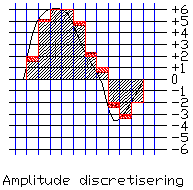
Fig 6 demonstreert de amplitude discretisering en de afrondingsfouten daarbij.

De horizontale lijnen geven de mogelijke getallen aan. De rode gebiedjes geven de afrondingsfouten aan. Deze afrondingsfouten zijn bij een praktisch signaal willekeurig, maar nooit groter dan + of - 0.5 eenheid. Omdat ze willekeurig zijn manifesteren ze zich als een witte ruis. Deze ruis wordt de "Kwantiserings ruis" genoemd.

Als Hifi enthousiasten hebben we meestal niet met de A/D conversie te maken, maar vooral  met de D/A conversie.

Een D/A converter doet eigenlijk niet anders dan de getallen die bij de A/D conversie verkregen zijn omzetten in evenredige elektrische spanningen.

Dat ziet er dan zo uit: (gearceerde kolommen)

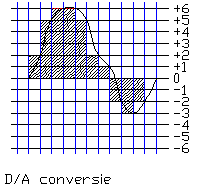
Fig 7

Op het eerste gezicht ziet dit er nogal hakkelig uit, maar dat komt doordat het hele spectrum van fig. 3 hier aanwezig is.

Met een laagdoorlaat filter, vergelijkbaar als dat bij de A/D conversie, ontstaat de vloeiende golfvorm.

Ook hier geldt weer dat een analoog laagdoorlaatfilter dat frequenties tot 20 Khz niet aantast en toch de frequenties boven 22 Khz goed onderdrukt niet eenvoudig te maken is.

En ook hiervoor is een goede oplossing gevonden door het filter uit te voeren in het digitale domein. Door tussen de samples van 44 kHz lineair te interpoleren wordt de sample frequentie drastisch verhoogd. Bij deze hoge sample frequentie kan een erg goed digitaal laag-doorlaat filter gemaakt worden.

Vervolgens vindt de feitelijke D/A conversie plaats op die hoge sample frequentie. Het benodigde analoge filter is dan vrij eenvoudig, want het hoeft alleen die hoge klokfrequentie te onderdrukken.

Ook hier geldt dat bij een voldoend verhoogde sample frequentie de resolutie van de feitelijke D/A converter minder kan zijn dan 16 bit. Ultimo resulteert dit in de 1-bit converters zoals die tegenwoordig vrijwel uitsluitend toegepast worden.

Als je goed kijkt zie je dat de golfvorm van fig. 7 wat afwijkt van die van fig. 1. Dat betekent niet dat er vervorming opgetreden is. Het is de bijdrage van de quantiseringsruis die in het voorbeeld hier aanzienlijk is omdat er zo weinig discretiserings nivo's gebruikt worden. Als het signaal van fig 1 wat in tijd verschoven zou zijn zouden de rode gebiedjes van fig 6 op andere plaatsen liggen en zou de golfvorm van fig 7 er weer anders uitzien. Dit is de willekeurige bijdrage van die quantiserings ruis.

Er is een software programma beschikbaar waarmee je zelf mogelijk wat experimenten kunt doen.

Hierover zal ik op een later tijdstip een summiere uiteenzetting geven.

In de audio techniek komen we regelmatig de begrippen Dynamiek, Dynamisch bereik en Resolutie tegen.

Dynamiek  (het woord betekent eigenlijk: beweeglijkheid) is de verhouding tussen de zachtste en de hardste passages in een muziekstuk, of in een opname daarvan.

Het Dynamisch Bereik van een audio apparaat is de verhouding tussen het sterkste geluid of elektrische signaal dat onvervormd doorgegeven kan worden, en de ruis en andere bijgeluiden die aanwezig zijn bij afwezigheid van signaal.

De termen Dynamiek en Dynamisch bereik worden nog wel eens door elkaar gebruikt. Getalsmatig worden ze altijd uitgedrukt in decibel

Praktische waarden voor de dynamiek zijn:  zo'n 40 dB voor de meeste "klassieke" muziek met grote volume verschillen, een enkele keer wat meer. Jazz en Pop muziek hebben meestal veel minder dynamiek, alhoewel er in generaal-pauzes wel sprake kan zijn van een "diepe stilte". Niet zelden kun je dan gebreken in de opname of het medium horen.

De begrippen Dynamiek en Dynamisch bereik zijn van toepassing op zowel analoge als digitale media en signaal-overdracht.

Het begrip Resolutie is alleen van toepassing op digitale overdracht of -media.

Bij Resolutie gaat het om het aantal discretiserings-nivo's dat voor het onderhavige signaal gebruikt wordt. Bij het 16 bit CD-systeem worden ruim 65000 nivo's gebruikt voor signalen met de maximale sterkte. De zwakste signalen in een klassiek orkestwerk met een dynamiek van 40 dB krijgen derhalve maar zo'n 500 nivo's. (een honderdste)

Is dat genoeg? Sommigen zeggen van niet. Maar bij die resolutie van 500 nivo's hoort een principieel ruisnivo van -56 dB.  Dat is een dynamisch bereik waarop iedere vinylplaat en de meeste zeer goede band-opnemers uit de 70-er jaren jaloers op kunnen zijn.

Verwar het begrip "resolutie" zoals ik dat hier gebruik niet met de mate waarin je in een muziekstuk allerlei details kunt horen. Het is weliswaar zo dat bij een slechte resolutie het "detail" verloren kan gaan, maar dat is dan door teveel ruis of intermodulatie vervorming, of door een matig tijd-gedrag van het systeem..