In het kort:
Er bestaat een eenvoudig te onthouden sommetje voor het verband tussen de tijdconstante van een 1ste orde filter en het 3 dB kantelpunt van de frequentie-overdracht.
kHz = 160 / usec, of usec = 160 / kHz
Let wel: Het hier beschrevene gaat alleeen op voor 1ste orde filters. Voor hogere orde filters kan het soms als een benadering gebruikt worden.
Verwar ook de begrippen Stijgtijd, Daaltijd, en Slew-rate niet met het hier beschrevene.
Verwante onderwerpen:
Filters, Amplitude- of Frequentie karakteristiek, Weerstand, Capaciteit, Zelfinductie
Hoog- en laagdoorlaat filters zijn combinaties van weerstanden, condensatoren en / of spoelen die hoge danwel lage frequenties doorlaten en de rest onderdrukken.
Hieronder de eenvoudigste, maar meest voorkomende 1e orde filters.
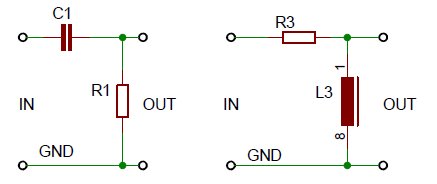
2 vormen van een High-Pass filter, dat de hoge frequenties doorlaat en de lage onderdrukt.
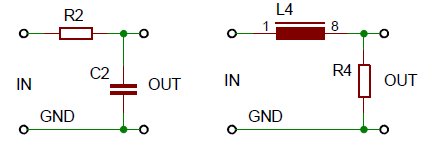
2 vormen van een Low-Pass filter, dat de lage frequenties doorlaat en de hoge onderdrukt.
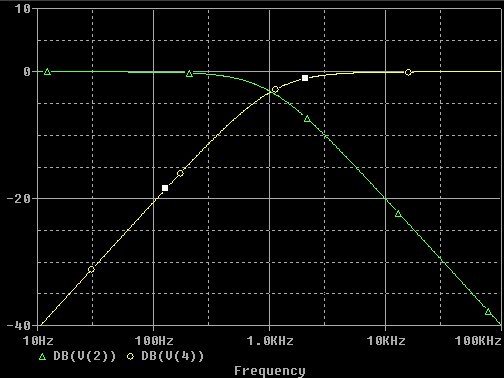
De overdracht als functie van de frequentie. Geel = hoogdoorlaatfilter, groen = laagdoorlaatfilter.
Beide filters hebben het -3dB kantelpunt op 1 kHz. In het onderdrukte gebied is de helling 6 dB/okt of 20 dB/decade.
Afleiding: Voor beide schakelingen met condensator geldt fk = 1 / 2πRC, en voor de schakelingen met zelfinductie geldt fk = R / 2πL.
Het product RC en het quotiënt L / R hebben beide de dimensie tijd, en we noemen dat de tijdconstante Tc van het filter.
We kunnen dus voor alle (1ste orde) filters schrijven fk = 1 / 2πTc
Halen we de 2π van onder de deelstreep naar boven dan wordt het 0.16, of 160 als we het nog eens met 1000 vermenigvuldigen.
Dan moet er ergens anders nog een keer door 1000 gedeeld worden, en dat doen we door de keuze van de eenheden.
We komen dan tot het volgende tabelletje:
| Frequentie | Tijdconstante | R | C | L |
| kHz | usec | kOhm Ohm |
nF uF |
|
| kHz | usec | Ohm | uH | |
| Hz | msec | kOhm Ohm |
uF mF |
|
| Hz | msec | Ohm | mH |
Je hoeft dus alleen te onthouden: kHz = 160 / usec, of usec = 160 / kHz en kHz wordt Hz als usec msec wordt.
(159 i.p.v. 160 is nog iets nauwkeuriger)
Ik heb hier alleen de relaties gegeven voor de meest voorkomende situaties in de audio praktijk. Bij passieve luidspreker wisselfilters zul je meestal met Ohms willen werken en zelfinducties gebruiken, bij actieve filters gebruik je meestal weerstanden in het kOhm bereik en condensatoren in het nF of pF bereik.
Een voorbeeldje voor een lange signaalkabel, bijv. om de muziek ook in een andere kamer te kunnnen horen via een versterker en luidsprekers ter plekke.
Zo'n kabel werkt in combinatie met de uitgangsimpedantie van de signaalbron als een laagdoorlaat filter.
Stel de kabellengte op 20 meter en de kabelcapaciteit op 400 pF per meter. We krijgen dan 8000 pF of 8 nF.
Stel de uitgangsimpedantie van de Line-Out uitgang van de signaalbron op 100 Ohm, of 0.1 kOhm.
De tijdconstante is dan 8nF x 0.1kOhm = 0.8 usec en de kantelfrequentie wordt dan 160 / 0.8 = 200 kHz.
Nog iets over de tijdconstante:
Hieronder staan de signalen in de tijd uitgedrukt, dus zoals je ze op een oscilloscope zou zien.
In beide gevallen is er aan de ingang van het filter een blokgolf van 0.5 kHz en 1 Volt pp toegevoerd.
De tijdconstante is nu de tijd die verstrijkt tot het signaal 63% van de eindwaarde heeft bereikt.
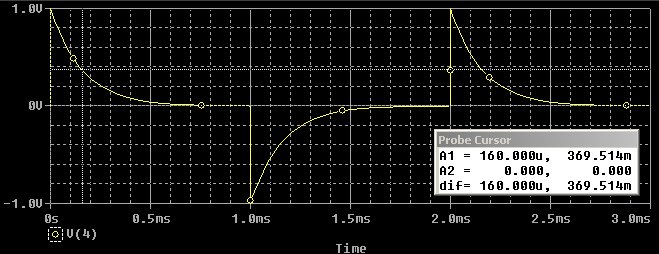
Blokgolf door het hoogdoorlaat filter. Het signaal begon op 1 Volt, de eindwaarde is 0 Volt, en 63% daarvan is dan 1V - 0,63V = 0.37 Volt.
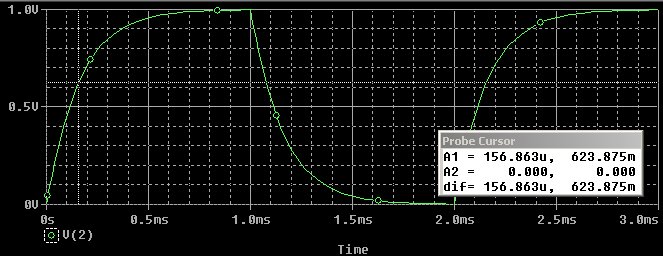
Blokgolf door het laagdoorlaat filter. Het signaal begint hier op 0 Volt, de eindwaarde is 1 Volt, en 63% daarvan is 0.63 Volt
(het lukte hier niet om de cursor exact op 160 ms te krijgen)
.