In het kort:
Er is vrijwel geen enkele luidspreker (chassis) die in z'n ééntje het hele bereik van audiofrequenties kan weergeven. We gebruiken meestal twee of meer luidsprekers die ieder een beperkt deel van het bereik goed kunnen weergeven. Er is dan op één of andere manier een filter nodig dat ervoor zorgt dat elke luidspreker het bereik toegevoerd krijgt dat 'ie kan weergeven.
Dit hoofdstuk bespreekt de alom toegepaste passieve wisselfilters, dus circuits tussen de versterker en de luidsprekers. Vrijwel altijd is dat filter in de luidsprekerkast ingebouwd.
Verwante onderwerpen:
Impulsgedrag
De componenten van een wisselfilter
Enkele begrippen in verband met filters.
Enkele benaderende berekeningen.
Meerdere identieke luidprekers
Luidsprekers met verschillende gevoeligheid en/of impedantie
Zobel netwerken: Compensatie van de luidspreker impedantie
Het transiënt gedrag van passieve wisselfiltersgrootte
De componenten van een wisselfilter
Een spoel (een klos koperdraad) of zelfinductie vormt een schijnbare weerstand die toeneemt met de frequentie. Als je een spoel in serie zet met een luidspreker zal 'ie de hoge tonen tegenhouden. Paralell aan een luidspreker worden de lage frequenties erdoor kortgesloten.
De grootte van een zelfinductie wordt opgegeven in Henry, evt. met het voorvoegsel milli voor een duizendste (mH) of micro voor een miljoenste (µH)
Dat kortsluiten bij lage frequenties gaat in de praktijk niet helemaal goed, want een spoel heeft altijd ook een bepaalde weerstand, simpelweg de weerstand van het gebruikte koperdraad. Omdat spoelen die bij lage frequenties werkzaam moeten zijn veel windingen nodig hebben moeten die met relatief dik koperdraad gewikkeld worden om die weerstand laag te houden.
In een aantal gevallen vind je daarom wel spoelen die gewikkeld zijn rond een ijzerkern. Er zijn dan voor de zelfde zelfinductie veel minder wikkelingen nodig, waardoor de weerstand van de spoel gemakkelijker laag kan blijven. Helaas zijn de magnetische eigenschappen van ijzer (permeabiliteit, hysteresis en verzadiging) afhankelijk van de stroom door de spoel. Dit betekent dat er intermodulatie vervorming kan optreden.
Voor hifi toepassingen gebruiken we liever geen spoelen met ijzer of zoiets er in. (De tussenvorm met een ijzerkern met luchtspleet heeft minder last van deze vervormingen)
Er worden hier en daar spoelen aangeboden gebaseerd op litze-draad, d.w.z. dat de draad bestaat uit een groot aantal apart geisoleerde dunne draadjes die afwisselend aan de buitenkant van de bundel komen en dan weer de diepte in gaan. Dit is een effectieve manier om het z.g. Skin-effect tegen te gaan. Bij spoelen voor wisselfilters is dit echter "het paard achter de wagen spannen". Het gaat er hier om een hoge impedantie te krijgen bij hoge frequenties. Het skin-effect helpt hier juist bij.
Spoelen met litze- draad gebruik je in filters die een zeer hoge Q-factor moetn hebben, zoals in afstemkringen van radio ontvangers.
Een condensator of capaciteit vormt een schijnbare weerstand die afneemt met de frequentie. Als je een condensator in serie zet met een luidspreker zal 'ie de lage frequenties tegenhouden. Paralell aan een luidspreker vormt 'ie een kortsluiting voor hoge frequenties.
De grootte van een condensator wordt opgegeven in Farad (F), meestal met een voorvoegsel als milli, micro, nano, pico, iedere keer duizend keer kleiner.
Condensatoren komen met uiteenlopende constructies en gebruikte materialen. Zo zijn er de electrolytische condensatoren, of elco's. (zowel gebaseerd op aluminium als op tantaal) Deze zijn goed verkrijgbaar en goedkoop, ook bij de wat grotere waardes (tientallen µF) die soms nodig zijn. Het nadeel van elco's is dat ze polair zijn, d.w.z. de spanning mag maar in 1 richting staan. Dit maakt de gewone elco onbruikbaar voor een wisselfilter. Er zijn wel bipolaire elco's te koop, maar deze bestaan uit twee gewone elco's tegen elkaar in in serie. Bovendien komen elco's met een vrij grote tolerantie op de waarde, en die waarde loopt in de loop der jaren nog wel eens terug ook.
Niet gebruiken dus.
Andere condensator typen worden meestal aangeduid naar het materiaal dat voor de isolatie, het diëlectricum gebruikt is. Ruwweg onder te verdelen in keramieken en polymeren (plastics).
Keramische condensatoren zijn niet goed verkrijgbaar in de waardes die je in wisselfilters doorgaans nodig hebt. Blijven de polymeren en papier.
De bekendste zijn hier polyethyleen, polycarbonaat, polyphenyleen sulfide, polystyreen, en polypropyleen. Deze materialen brengen bepaalde verschillen in eigenschappen met zich mee, maar die zijn bij wisselfilters niet van belang.
Voor condensatoren geldt verder dat ze altijd komen met een maximale werkspanning.Voor een wisselfilter is zo'n 60 Volt altijd genoeg. Meer is wel duurder, maar niet beter. (er gaat in hifi kringen het verhaal dat een condensator van (veel) hogere werkspanning "beter zou klinken". Daar is een terecht argument voor: Je blijft dan verder weg van de doorslagspanning en daardoor zullen evt. niet lineariteiten -de capaciteit kan ietwat spanningsaf hankelijk zijn- geringer zijn. Deze effecten zijn echter zo gering dat die onhoorbaar zullen zijn.
Weerstanden worden gebruikt om aanpassingen te maken voor gevoeligheids verschillen tussen de diverse luidsprekers. Een enkele keer is dit zelfs regelbaar uitgevoerd, dat lijkt me nogal ongewenst, want dan weet je nooit echt goed hoe het staat.
Omdat er soms flinke vermogens in het spel zijn worden hier draadgewonden weerstanden gebruikt. Vaak ingebed in keramiek, (cermet) om de warmte geleiding te verbeteren. Het steekwoord voor zulke weerstandscombinaties is "L-Pad".
Gloeilampen, of sterk daar op lijkende dingen zoals een glazen buis met een al-of-niet gewikkelde draad daarin, zie je nog wel eens in disco luidsprekers. De achtergrond is dat de weerstand van zo'n gloeilamp sterk stijgt als de gloeidraad heter wordt, en daarmee kun je de luidsprekers beschermen tegen overbelasting.
De lampen worden nog wel eens aan de voorkant geplaatst, zodat je ze kunt zien oplichten als de luidspreker te zwaar belast wordt.
In huiskamer- hifi apparatuur horen zulke dingen niet thuis. Bij de lage frequenties van een basluidspreker kunnen ze intermodulatie vervorming veroorzaken, en bij hogere frequenties gaan ze als een soort limiter werken. Om oversturing van je luidsprekers te voorkomen moet je je oren gebruiken, en ook wat daartussen zit.
Een zekering (smeltveiligheid) wordt soms in een luidsprekerkast gemonteerd om de luidsprekers te beschermen tegen overbelasting. Omdat smeltveiligheden in dit verband veel gemeen hebben met gloeilampen -temperatuur afhankelijke weerstand- horen ze naar mijn smaak ook niet thuis in hifi luidsprekers.
Enkele begrippen in verband met filters.
We kennen 5 basis
typen filters.
- Low pass, of laag doorlaatfilter. Laat lage frequenties door, houdt hoge frequenties tegen
- High pass, of hoog doorlaatfilter. Laat hoge frequenties door, houdt lage frequenties tegen
- Band pass, of band doorlaatfilter. Onderdrukt hoge en lage frequenties, maar laat ergens daartussen een frequentie gebied door.
- Band stop, of band sperfilter. Laat hoge en lage frequenties door, maar onderdrukt een deel van het middengebied.
- All pass. Dit filter laat alle frequenties even sterk door, maar het doet iets met de fase en de looptijden.
Bij alle filters (behalve de all-pass) hebben we met de volgende eigenschappen te maken:
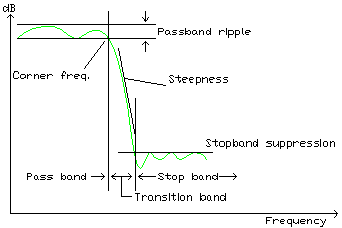
Fig 1.
We zien hier als voorbeeld de karakteristiek van een laag doorlaat filter. Op de vertikale as staat de uitgangs signaalsterkte in dB, op de horizintale as de frequentie op een logarithmische schaal.
We onderscheiden 3 frequentie gebieden: de doorlaat-band, de onderdrukkings band, en het overgangs gebied daartussen.
In de doorlaat band is er meestal wat onregelmatigheid in de karakteristiek, de passband ripple.
Bij de corner frequency of kantelfrequentie begint de eigenlijke overgang. Meestal definieren we die bij een verzwakking van 3dB ten opzichte van de doorlaatband.
In de stopband blijken veel filters ook een rimpel te hebben. De frequentie die nog het sterkst doorgelaten wordt bepaalt de stopband onderdrukking.
De helling van de karakteristiek in het overgangsgebied noemen we de steilheid (eng: steepness). Deze steilheid wordt meestal uitgedrukt in dB/octaaf, oftewel hoeveel dB het signaal verzwakt is bij de dubbele of halve frequentie.
Die steilheid hangt nauw samen met de"orde" van het filter. Een 1e orde filter heeft een steilheid van 6 dB/oct, een 2e orde 12 dB/oct, en voor elke orde komt er weer 6 dB/oct bij.
Je kunt de orde, en dus de steilheid van het filter ongeveer aflezen aan het totaal aantal spoelen en condensatoren dat er voor een overgangs band gebruikt is. (weerstanden tellen niet mee voor de orde bepaling)
Bedenk daarbij dat bijv. een band doorlaat filter eigenlijk een combinatie is van een laag- en een hoog- doorlaat filter. Zo'n filter kan best voor de hoge kant een andere orde hebben dan voor de lage kant.
Noot: De relatie tussen het aantal spoelen + condensatoren, de orde en de steilheid gaat niet meer op voor filters die nadrukkelijk op resonatie kringen berusten (filters met hoge Q-factor). Zulke filters hebben doorgaans een slecht impulsgedrag, dus die wil je niet gebruiken
Butterword, Chebychef, Bessel en zo
Deze namen zijn historisch verbonden aan de filter theorie, en in het bijzonder aan het optimaliseren van bepaalde eigenschappen van een filter.
Zo probeert Butterworth de doorlaat band zo vlak mogelijk te krijgen. In het overgangs gebied treden echter aanzienlijke fase fouten op.
Chebyshev (ja, verschillende bronnen spellen de naam verschillend) concentreert zich op een gelijkmatige rimpel in de doorlaatband en een steile helling.
Bessel probeert de looptijden in de doorlaatband en de overgangsband redelijk constant te houden. Dit wordt ook wel "lineaire fase" of "constante fase" genoemd. De prijs die je er voor betaalt is een geringere steilheid in de overgangsband, en wat minder onderdrukking in de stop-band.
Andere namen in dit
verband zijn o.m.: Boode, Cauer, Gauss, Linkwitz.
Het is niet zo dat je aan een filterschakeling zo kunt zien met welk type je te maken hebt. Filters met dezelfde topologie (de manier waarop de onderdelen geschakeld zijn) kunnen best heel verschillende karakteristieken hebben, afhankelijk van de waarde van de onderdelen. Andersom, kunnen dezelfde karakteristieken soms met verschillende topologien gerealiseerd worden.
Ik heb voor de
voorbeelden een 3-weg systeem gekozen omdat daarin de meeste basis-filters
voorkomen: laag-doorlaat, band-doorlaat en hoog-doorlaat.
In een twee-weg systeem kun je de circuits voor de middentonen wegdenken.
Hieronder zien we het eenvoudigste filter:
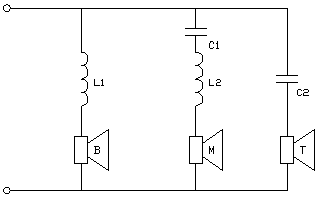
Fig 2.
Er is een zelfinductie L1 die de hoge tonen naar de basluidspreker B tegenhoudt, de condensator C2 laat alleen de hoogste frequenties door naar de tweeter T, en de combinatie van C1 en L1 houdt zowel de hoogste als de laagste frequenties tegen naar de middentoon luidspreker M.
De wat geïdealiseerde frequentie karakteristieken zijn hieronder te zien: (Blauw: bas, Groen: midden, Rood: tweeter)

Fig 3.
Bij deze eenvoudige schakeling is de steilheid waarmee het signaal overgaat van de ene naar de andere luidspreker nogal slap. Dat betekent dat de luidsprekers relatief veel signaal zullen ontvangen wat eigenlijk voor een andere luidspreker bedoeld is.
Dit is een "eerste orde" filter of een filter met een helling of steilheid van 6 dB/octaaf.
In fig 4. zien we hoe dit verbeterd kan worden.
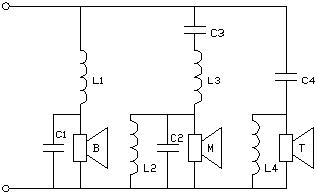
Fig 4.
Ten opzicht van fig 2. is er een extra C1 die hogere frequenties naar de basluispreker kortsluit. Op dezelfde manier sluit L4 de lagere frequenties naar de tweeter T kort.
C2 en L2 werken op vergelijkbare wijze voor de middentoner M.
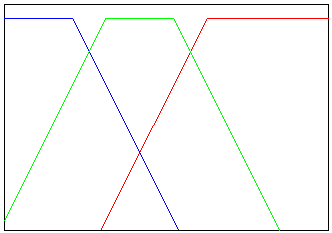
Fig 5.
De overdracht van het "tweede orde systeem" van fig. 4, een filter met hellingen van 12 dB/octaaf. De "buur" luidsprekers ontvangen al beduidend minder signaal wat niet voor hen bestemd is.
En zo kunnen we nog wel wat verder gaan. Je komt wel wisselfilters met de 4e orde tegen, oftewel 24 dB/octaaf, zoals hieronder.
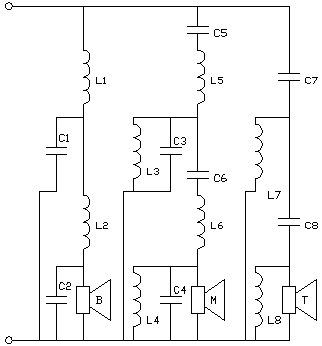
Fig 6. Een 4e orde filter
Het is ook niet ongebruikelijk dat de diverse luidspreker-groepen filters van verschillende orde hebben.
Wat zijn de voor en/of nadelen van zulke hogere orde filters?
Het voordeel is dat de luidsprekers slechts weinig signaal ontvangen dat niet voor hen bedoeld is. Dat is vooral een kwestie van smaak, en het hangt samen met de keuze van de luidsprekers. Om een voorbeeld te geven: Sommige basluidsprekers geven best nog flink wat midden tonen weer. Meestal echter met een sterke "kleuring". In zo'n geval wil je niet dat er veel midden en hoog in het baskanaal komt.
Het nadeel is dat er -vooral op de overgangen van de ene naar de andere luidspreker- grote fasefouten optreden. Dat gaat altijd gepaard met een slechte impuls responsie. Bovendien zullen sommige frequenties tegenfasig uit de luidsprekers komen en elkaar uitdoven. En dat is wel goed hoorbaar als een ongewenste "kleuring" van het geluid.
Een bijkomend nadeel
is dat hogere orde filters vaak kritischer zijn voor de juiste waarde van de
componenten. Je komt dan soms met de reekswaardes
waarin spoelen en condensatoren verkrijgbaar zijn niet goed uit.
Iemand die het weten kan verzekerde me dat je met filters van meer dan
de tweede orde het tijdgedrag van het systeem niet goed kan krijgen.
Enkele benaderende berekeningen.
Deze paragraaf geeft slechts enkele benaderingen om "op een hoekje van de krant" te kunnen uitrekenen wat ongeveer de kantelfrequentie van een filter is, c.q. welke zelfinductie of capaciteit daarvoor nodig is. Ik geef alleen de benaderings formules voor 1e en 2e orde filters. Bij hogere orde filters is de onderlinge beinvloeding van de componenenten zodanig dat er een onbedrukte krant voor nodig is.
Bij gebrek aan betere gegevens beschouw ik de luidspreker steeds als een zuivere weerstand (Zie het Zobel netwerk).
Voor een eerste orde L-R (low-pass) of een R-C (high-pass) filter zoals in fig. 2 geldt dat de kantelfrequentie op de plek ligt waar de schijnbare weerstand van de zelfinductie (xL)of de capaciteit (xC) gelijk is aan de weerstand van de luidspreker.
Voor de 8 Ohm bas luidspreker kiezen we bijv. een kantelfrequentie van 200 Hz.
De schijnbare weerstand van een zelfinductie is xL = 2*pi*f*L (Ohms), waarbij pi = 3.14, f de frequentie in Hz en L de zelfinductie in Henry.
Omgewerkt: L = xL / (2*pi*f) of: L = 8 / (2*pi*200) = 6.34 mH
Voor de 8 Ohm tweeter kiezen we bijv. 3 Khz als scheidings frequentie.
De schijnbare weerstand van een condensator is xC = 1/(2*pi*f*C) (Ohms) waarbij pi = 3.14, f de frequentie in Hz en C de capaciteit in Farad.
Omgewerkt: C = 1 / (2*pi*f*xC) of: C = 1 / (2*pi*3000*8) = 6.63 E-6 oftewel 6.63 micro Farad.
Op soortgelijke wijze kun je ook benaderende berekeningen maken voor middentoners of luidsprekers met andere impedanties.
Het "fine tunen" van een filter is echter een klus om met hulp van een computerprogramma te doen.
Er zijn computerprogramma's in omloop die speciaal gericht zijn op wisselfilters. Sommige kennen ook eigenschappen van bekende luidsprekers, misschien zelfs wel als ze in een kast gemonteerd zijn. (Dit maakt voor bas- en middentoners nogal wat uit. Tweeters zijn vrijwel altijd dicht aan de achterkant en dan maakt de kast niet veel uit voor het impedantie verloop)
Voor het simuleren volstaat een programma dat slechts lineaire elementen aan kan. Ook het aantal componenten is niet zo erg groot, dus je kunt uit de voeten met een demo-versie van een veel duurder pakket voor elektronica simulatie, zoals pSpice Student.
In eenvoudige boxjes
zie je nog wel eens een schakeling als deze: (links)
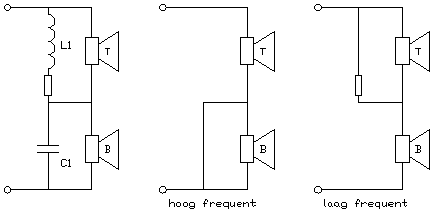
Fig 11.
Op het eerste gezicht lijkt het alsof we met een tweede orde filter te doen hebben, waarbij zowel de spoel als de condensator dubbel gebruikt zijn. Dat is echter schijn, want als bijv. bij toenenemde frequentie xL groter wordt dan de weerstand van de tweeter dan worden de tweeter met C1 bepalend voor de steilheid.
Er zit echter meer venijn in dit circuit:
Ik heb er de onvermijdbare serieweerstand van de spoel ingetekend om duidelijk te maken waar het fout gaat.
Voor hoge frequenties gaat de linker schakeling over in de middelste. De basluidspreker wordt kortgesloten door de condensator, en de zelfinductie vertegenwoordigt een hoge impedantie, dus is praktisch afwezig. Dit gaat wel goed.
Bij lage frequenties (meest rechtse schakeling) is de spoel echter niet in staat om de tweeter goed kort te sluiten, want de spoel weerstand blijft steeds aanwezig.
De tweeter kan daarom nog een substantiele portie laag krijgen, en daar kunnen ze meestal slecht tegen.
Wees altijd op je hoede als je luidsprekers in serie ziet staan.
Ik heb eens een lezing bijgewoond van iemand die vond je alleen maar filters moest gebruiken waarbij de luidsprekers in serie staan. Hij raakte dus helemaal in de knoop toen hij probeerde om er 2e- of hogere ordes mee te maken, want dat kan niet zolang de luidsprekers in serie staan. Hattienietdoor.
Meerdere identieke luidprekers
Tweeters en
middentoners worden nog wel een verdubbeld of nog meer. Meestal is dat gedaan om
het maximale vermogen dat de kast kan verwerken te vergroten. Tenzij je
house-parties wilt gaan organiseren moet je je afvragen of dat zo zinvol is.
Vrijwel alle luidsprekers kunnen vermogens verwerken die ruimschoots voldoende
zijn voor huiskamer hifi, evt met een burenruzie.
Bovendien wordt het richt effect versterkt in het vlak waarin de luidsprekers 'op een rij' staan. Bijv. een rijtje tweeters boven elkaar zal een sterk richt effect vertonen in het vertikale vlak.
Staan de luidsprekers echter opgesteld in een bol kan er zelfs een 'rondom straler' gemaakt worden.
De volgende figuren illustreren deze stralings eigenschappen.
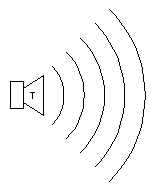
Fig 12.
Stralings patroon van een luidspreker, als het stralend deel van de conus wat kleiner is dan de golflengte.
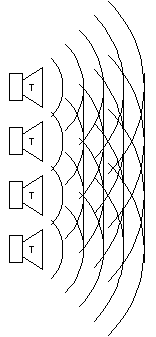
Fig 13
Stralings patroon van een rijtje luidsprekers, als de golflengte in de ordegrootte van de onderlinge afstand ligt. Je ziet dat er een min of meer vlak golffront ontstaat.
Als de afstand tussen de luidsprekers meerdere golflengtes bedraagt kunnen er op enige afstand uitdovingen of versterkingen optreden. (interferentie)
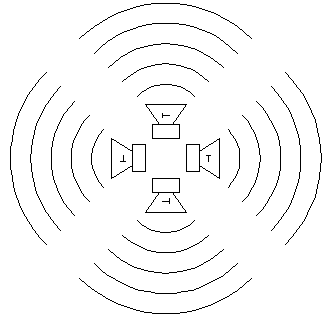
Fig 14.
Stralings patroon van een bolstraler.
In deze voorbeelden zijn de luidsprekers met gelijke polariteit aangestuurd. Je kunt je wellicht voorstellen dat het stralings patroon aanzienlijk verandert als er 1 tussen zit met omgekeerde polariteit.
Meerdere identieke basluidsprekers
Ook dit wordt nog wel eens gedaan om een groter maximaal vermogen te kunnen hanteren. Hetgeen op zich zelden nodig is, maar er zijn meer en andere voordelen aan verbonden.
Vooropgesteld dat de luidsprekers dicht bij elkaar gemonteerd zijn zou zo'n samenstel een lagere resonantie frequentie hebben dan bij een enkele luidspreker (ik heb hiervan nog geen theoretische verificatie gezien). Als dit klopt is dat voordelig, want luidsprekers produceren nu eenmaal zeer weinig geluid beneden hun eigen resonantie frequentie.
Een tweede voordeel is dat bij het zelfde afgestraalde vermogen de conus uitslag geringer is. Dit voordeel vertaalt zich onmiddelijk in lagere intermodulatie vervorming, want bij een grote conus uitslag komt de spreekspoel in een gebied waar het magneetveld minder is Bij middentoners en tweeters speelt dit probleem niet, aangezien de slag daar zeer veel kleiner is.
Je hoeft bij meerdere identieke basluidsprekers niet bang te zijn voor problemen met richting effecten. In vergelijking met de golflengte zijn basluidsprekers altijd klein en zitten dicht bij elkaar. Daarom gedragen ze zich ook gezamenlijk als één rond-om straler.
Meerdere identieke luidsprekers opnemen in een wisselfilter
Als je meerdere identieke luidsprekers wilt toepassen moeten die ook op een geschikte manier aangesloten worden. Hierbij moet je vooral ook kijken of de demping van de luidsprekers niet om zeep geholpen wordt.
Het is verleidelijk om bijv. 4 identiek luidsprekers zo te schakelen:
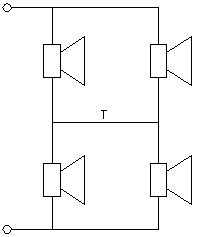
Fig 15.
Zo geschakeld hebben 4 identieke luidsprekers een vervangings impedantie gelijk aan die van 1 luidspreker. De verbinding T lijkt eigenlijk niet eens nodig.
Als deze luidsprekers ook op een identieke manier uitslingeren zullen ze gelijk-op gedempt worden door de versterker.
Echter, ook eendere luidsprekers zijn nooit precies identiek, en er kunnen verschillen in uitslinger gedrag zijn.
Laat in ieder geval de verbinding T in takt. Deze bewerkstelligt dat iedere luidspreker tenminste de paralellschakeling van 3 andere ziet (aangenomen dat de versterker een zeer lage impedantie heeft)
Bij 2 identieke luidsprekers zit er niets anders op dan ze paralell te schakelen. Serieschakelen geeft grotere problemen met de demping.
Je kunt op zoek gaan naar twee 16 Ohm luidsprekers, of genoegen nemen met 8 Ohm en dan dus eindigen met een 4 Ohm systeem. Je versterker moet dat kunnen hebben, en mogelijk moet je dikkere luidspreker kabels gebruiken.
Luidsprekers met verschillende gevoeligheid en/of impedantie
De gevoeligheid van
luidsprekers wordt opgegeven als de geluidssterkte die de luidspreker produceert
bij 1 watt ingangs vermogen op 1 meter afstand.
Veel luidsprekers geven zo'n 90 dBa.
Het gunstigst is natuurlijk om luidsprekers van gelijke gevoeligheid en gelijke impedantie te combineren.
Als je echter luidsprekers met verschillende impedantie door elkaar gebruikt moet je hier extra rekening mee houden.
Bijvoorbeeld, als je een 8 Ohm en een 4 Ohm speaker combineert zal de 4 Ohm luidspreker 6 dB meer geluid produceren, als ze beide bijv. 90 dBa/W zijn. De 4 Ohm luidspreker krijgt immers het dubbele vermogen ten opzichte van de 8 Ohmer.
Soms kies je een combinatie van luidsprekers op basis van een aantal interessante eigenschappen, maar blijken ze door verschillen in gevoeligheid toch niet goed bij elkaar te passen.
Je kunt dan een aanpassing maken door het gebruik van weerstanden.
Ook hier moet je erg letten op het effect dat een weerstands netwerk heeft op de demping van de luidspreker.
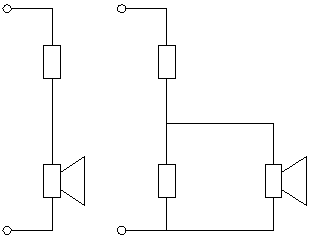
Fig 16.
Het linker schema geeft de meest simpele manier aan om een te gevoelige luidspreker wat te verzwakken. De demping van de luidspreker komt hierbij in gevaar, zeker als de serie weerstand in de grootte orde komt van die van de luidspreker.
Het rechter schema geeft een betere manier van verzwakken aan. De luidspreker "ziet" de paralellschakeling van de weerstanden, waardoor de demping redelijk gehandhaafd kan blijven.
Je moet er wel wat
meer aan rekenen, maar je kunt dan ook bewerkstelligen dat de filter schakeling
nog steeds 8 Ohm ziet. Neem maar eens voor de bovenste weerstand 4 Ohm, en de
onderste weerstand -en de luidspreker- 8 Ohm. Het filter "ziet" dan
nog steeds 8 Ohm. De luidspreker "kijkt" in ca. 3 Ohm, en de
verzwakking is 6 dB.
Deze schakeling met 2 weerstanden wordt wel een L-pad genoemd.
Het Zobel netwerk: Compensatie van de luidspreker impedantie.
Een luidspreker
vertoont steevast een wat grillig verloop van z'n impedantie. Een 8 Ohm
luidspreker vertegenwoordigt bij gelijkstroom en extreem lage frequenties een
ohmse weerstand van ca. 5 a 6 Ohm. Bij wat hogere frequenties wordt de
impedantie inductief, om bij de eigenresonatie om te slaan naar capacitief. Bij
de eigenresonantie is de impedantie Ohms, maar kan gemakkelijk 20 tot 50 Ohm
bedragen. Dit hangt ook sterk af van de kast waarin de luidspreker gemonteerd
is. Beneden de resonantie frequentie straalt een luidspreker erg weinig geluid
af.
Bij frequenties boven de eigenresonantie neemt de impedantie weer af tot ongeveer 8 Ohm, om bij zeer hoge frequenties weer te gaan stijgen door de elektrische zelfinductie. Tengevolge van allerlei geringere resonanties in het conus materiaal kunnen er nog allerlei grillige maar doorgaans geringe variaties in de impedantie optreden.
Bij het berekenen van wisselfilters zitten die impedantie variaties nogal in de weg. De meest hinderlijke variaties kunnen gecompenseerd worden met netwerkjes die bekend staan als "Zobel" netwerken.
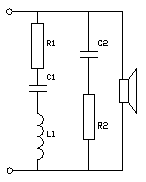
Fig 17. Luidspreker met een Zobel netwerk .
C1 en L1 vormen een
resonantie kring die afgestemd wordt op de eigenresonantie van de luidspreker in
de uiteindelijke kast. Met R1 wordt de weerstand bij resonantie bepaald. Het
komt er op neer dat bij resonantie R1 parallel aan de luidspreker staat. R1 zal
in de praktijk zo'n 10 a 20 Ohm zijn, bij 8 Ohm luidsprekers.
Voor L1 en C1 geldt dat de resonantie frequentie fr = 1/ (2 * pi *
wortel (L * C) ) oftewel: L * C = 1 / (2 * pi *
fr2)
De verhouding van L1 en C1 bepaalt de breedte van de resonantie piek. Als je C1 groter maakt, en L1 evenveel kleiner dan wordt de resonantie van het netwerk scherper. Andersom zal de piek breder worden.
C2 en R2 vormen een compensatie voor de elektrische zelfinductie van de luidspreker (spreekspoel). R2 is typisch in de buurt van 8 Ohm en C2 wordt zo gekozen dat C2 = Le / (R2 * Rnom)
Als je over een blokgolfgenerator en een oscilloscope beschikt kun je betrekkelijk eenvoudig de waardes experimenteel vaststellen. Sluit de blokgolf generator via een weerstand van bijv 1 kOhm aan op de luidspreker. Meet de spanning over de luidspreker met de scope. Varieer de frequentie om om de resonantie frequentie vast te stellen. (dit gaat nog beter als je de generator op sinusgolven zet). Zet de generator op blokgolven en op een ca. 10 x lagere frequentie. Je ziet op de scope het uitslingeren van de luidspreker resonantie. Experimenteer nu met L1 en C1 tot je zo weinig mogelijk uitslingeringen ziet.
Om C2 en R2 te bepalen zet je de blokgolf generator op een veel hogere frequentie en de scope op een veel kortere tijdbasis, zodat je de overshoot van de zelfinductie goed kunt zien.
De gedachte achter
multi-wiring berust geheel op een foute interpretatie van de elektrotechniek,
nl. dat hoge en lage frequenties elkaar in 1 kabel "in de weg" zouden
zitten. Het is daarmee niets anders dan verspilling van luidsprekerkabel.
Bi-wire adepten gebruiken meestal ook nog eens dure kabel soorten, dus tel uit
je winst als je niet meedoet met die onzin.
Voor bi/tri/multi wiring moeten de filters zo ontworpen zijn dat de luidsprekers elektrisch volledig van elkaar gescheiden zijn. Combinatie schakelingen als in fig 11 zijn niet geschikt voor multi-wiring.
In het onderstaande wordt e.e.a. verduidelijkt.
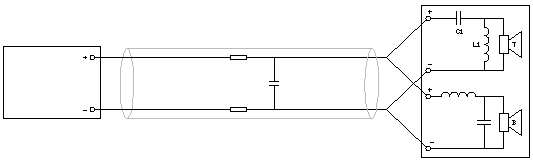
Fig 18.
"Normale" bedrading. Ik heb de serie impedantie van de kabel (weerstand, skin-effect en zelf-inductie) en de parallel capaciteit er in getekend.
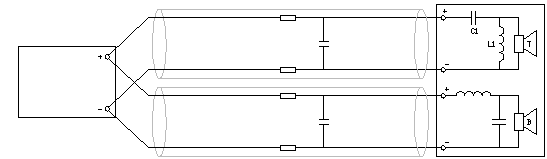
Fig 19.
De bi-wire bedrading.
Je ziet dat bij multi-wiring de kabelcapaciteit zoals de versterker die ziet toeneemt. Dit is zelden een probleem, maar het is niet nodig.
Ook voor de demping van de luidsprekers en de verliezen in de kabel heeft bi-wiring geen voordeel. In beide gevallen ondergaat het signaal naar iedere luidspreker het verlies door 1 kabel, c.q. "ziet" de luidspreker de weerstand van 1 kabel, en het doet er niet toe of dat 1 gezamenlijke kabel is, dan wel 2 of 3 aparte kabels.
Er is 1 situatie waarbij multi-wiring wat kan uitmaken, dat is als de secties van het wisselfilter onderling resonantie vertonen en je kabel een te hoge weerstand heeft. In het bi-wire geval zullen de effecten daarvan een beetje anders zijn. We hebben het dan over een kabel met een veel te hoge weerstand en een slecht ontworpen wisselfiler.
Als je reeds zulke kabels hebt liggen doe je er verstandig aan om bij de luidsprekerkasten de gelijke polen ook door te verbinden. Je hebt dan voor alle frequenties en alle luidsprekers de kabelweerstand verkleind. Gebruik niet de beide aders van de ene kabel voor héén en die van de andere voor terug, want dat geeft extra zelfinductie.
Hierover is er een aparte pagina
Het transiënt gedrag van passieve wisselfilters.
Hieronder geef ik enkele simulatie resultaten van een 1e orde en een 2e orde tweeweg filter.
In alle gevallen heb ik de luidsprekers als zuivere weerstanden van 8 Ohm verondersteld. In de praktijk is 'ie dat zeer beslist niet. Dat maakt het alleen maar erger, hoewel je de schade kunt beperken met een Zobel netwerkje.
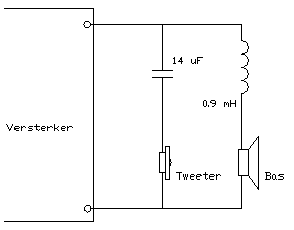
Fig20. 1e orde tweeweg filter
De component waardes zijn zo gekozen dat de kantelfrequenties c.q. de tijdconstantes van de hoog- en de laag sectie gelijk zijn. Alleen bij die conditie krijg je een vlakke amplitude en fase karakteristiek, en is ook het impulsgedrag goed.
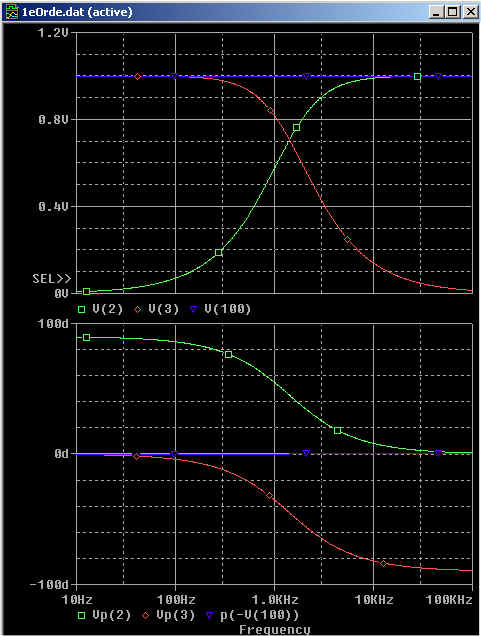
Fig 21. Amplitude en fase gedrag van het 1e orde filter.
groen: tweeter, rood: bas, blauw: sommatie van die twee.
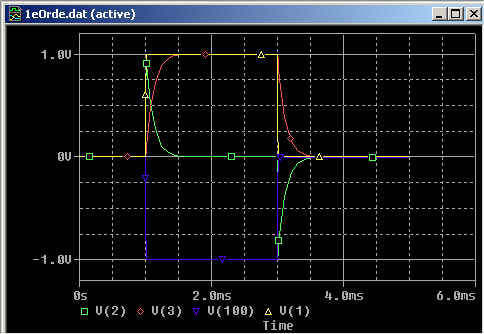
Fig 22. Respons op een enkele puls (blok) van 1 msec tijdsduur
geel: het ingangssignaal
Het som signaal staat hier omgekeerd. Dat komt doordat ik in de simulatie een inverterende sommeer versterker gebruikt heb.
We zien dat er met een 1e orde filter een perfect impulsgedrag bereikt kan worden, als de luidspreker impedantie maar een zuivere weerstand is. Dat is 'ie normaliter niet, maar die schade kun je enigszins beperken met Zobel netwerkjes aan iedere luidpreker. Verder moet de luidspreker natuurlijk alles perfect weergeven, en dat doen ze meestal ook niet.
Bij hogere orde filters is het fase- en impuls gedrag doorgaans veel slechter.
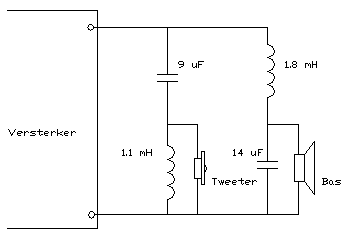
Fig23. Een 2e orde tweeweg filter

Fig 24. Amplitude en fase respons van het 2e orde filiter.
groen: tweeter, rood: bas, blauw: sommatie, geel: verschil
We zien in de sommatie (blauw) een forse dip. Dat is onvermijdelijk, want bij de overgangs frequentie draait het basfilter de fase ongeveer 90 graden de ene kant op, terwijl het hoog filter ca. 90 graden de andere kant op draait. In het fase diagram zie je de fase van het gesommeerde signaal dan ook de klok rond gaan. Door wat sleutelen aan de zelfinductie en capaciteiten kun je het nog wel wat beter krijgen, maar het komt nooit echt goed.
Velen komen hier in de verleiding om 1 van de luidsprekers om te polen. Je krijgt dan de gele curves, die er in de amplitude- en fase plaatjes minder erg uitzien.
Bekijken we echter het transient gedrag dan blijkt het in beide gevallen een rommeltje.
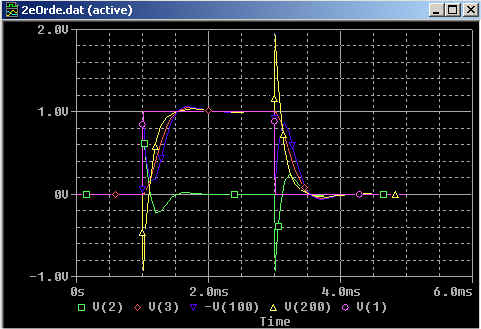
Fig 25 . Respons op een enkele puls (blok) van 1 msec tijdsduur.
paars: het ingangssignaal
We zien zowel in het verschil- als in het somsignaal aanzienlijke afwijkingen. Er valt mogelijk nog wat te optimaliseren aan dit filter, maar je krijgt het nooit goed.
Het is te verwachten dat als je de luidsprekers voorstelt met hun "echte" impedantie verloop het allemaal nog erger wordt. Met een Zobel netwerkje kun je die schade wel beperken, maar dat kost weer een handvol extra onderdelen.
.